Inkscape 226 – Gitterverformung 2, Pfadeffekt Infos
Inkscape-User wünschten sich etwas mehr Informationen zu dem Pfadeffekt Gitterverformung 2, denn es kann mühselig sein, Verformungen durch Ziehen an den Handles vorzunehmen. Verzerrungen über die Punkte-Eingabe ist leichter, wenn man das System kennt.
Skills: Easy
Plugin: Nein
Version: Ab Inkscape 0.92
Möchte man bei der Gitterverformung die Punkte über die Regler der Werte arbeiten haben einige das Problem die richtigen Handles auf Anhieb zu finden. Zu diesem Beitrag gibt es kein Beispiel, sondern es sollen hier nur die Punkte, beziehungsweise nur kurz das System erklärt werden um die Arbeit zügig verrichten zu können.
Gitterverformung 2
Der Pfadeffekt Gitterverformung 2 wird wie alle Pfadeffekte über Pfad – Pfadeffekte oder mit dem Shortcut SHIFT-STRG-7 aufgerufen. Aus der Liste der Effekte kann dann die Gitterverformung ausgewählt werden (siehe Bild unten).

Pfad – Pfadeffekte (SHIFT-STRG-7)
Gruppierte und/oder vereinte Zeichenobjekte lassen sich mit der Gitterverformung leicht vornehmen. Der Effekt legt dazu ein Raster mit Anfassern über die Zeichnung die verschoben und ein Objekt so verformt werden kann.

Use only Perimeter (Inkscape 1.0)
Aktiviert man die Option Use only Perimeter (erst ab Inkscape Version 1.0 verfügbar), bleiben zum Verformen nur noch die äußeren Nodes bestehen (siehe Animation unten).

Raster und deaktiviertes Raster innen
Das Raster hat immer 25 Punkte, die Anzahl kann nicht reduziert werden. Ausnahme ist, wenn man die oben beschriebene Option Use only Perimeter nutzt.
Es kann sehr viel leichter sein sich die Punkte einzublenden und eine Verformung über die Werte der Achsen X (horizontal) und Y (vertikal) vorzunehmen. Gerade, wenn man an den Anfassern zieht und sich die Live-Ansicht anzeigen lässt, kann es zu schweren Rucklern kommen die ein zielgerichtetes Arbeiten erschweren (siehe Bild unten).
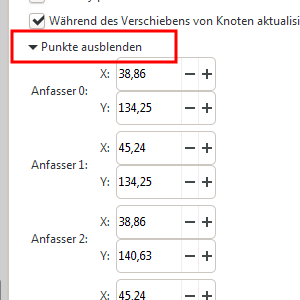
Punkte ein-/ausblenden
Man muss das System aber erst einmal durchschaut haben damit man zielgerichtet die gewünschten Nodes trifft die bearbeitet werden sollen. Verändert man dann die Werte dieser Punkte dann, so finden die Änderungen prompt und ruckelfrei statt.
Das System
Im Prinzip ist das System einfach. Zwar kann man es sich kompliziert machen, wenn man sich mit dem mathematischen Model dahinter beschäftigt, aber für die Anwendung kann man eine einfache Hilfe verwenden. Die Punkte liegen immer Z-förmig zueinander.
Dabei funktioniert die Z-Form immer von links nach rechts und stets auf gespiegelten Achsen (siehe Bild unten).

Punkte benannt in Z-Form
Man kann es sich leicht merken/vorstellen, wenn man sich eine solche Form aufzeichnet oder zumindest einmal an den Beispielen hier betrachtet hat. Gezählt wird von 0 (Null) an. Von 0 (Null) bis 3 ist das klar zu erkennen. Es geht dann weiter nach innen, auf der gleichen Reihe, bei den Punkten 4 bis 7 (siehe Bild oben). Immer verläuft die Reihenfolge in Richtung des Buchstaben Z (siehe Bild unten).

Z-förmig zueinander liegende Punkte
Eine Eigenart stellt die nächste Zahlenreihe dar. Punkt 8 hat auf der horizontalen Achse kein Gegenüber da er in der Mitte liegt, daher wird er als 8 und 9 bezeichnet. Auf der gegenüberliegenden Achse das Gleiche mit Punkt 10 und 11. Das muss man so hinnehmen. Diese beiden Punkte schließen dann auch Reihe 1 und 5, beides äußere (oben und unten) Reihen ab (siehe Bild unten).
Klarer geht es dann weiter mit Punkt 12 bis 15. Diese Zahlenreihe liegt außerdem außen und bildet den Anfang der nächsten Reihe (siehe Bild unten).

Eigenart bei Mittelpunkten
Letztendlich kann man sich die Zahlenreihe von 8 bis 11 allerdings auch als eine Z-Form vorstellen. Wie schon erwähnt muss man das einfach hinnehmen (siehe Bild unten).

Z-förmig denken
Weiter geht es indem man in der Reihe einen Punkt weiter nach innen rückt mit den Punkten von 16 bis 19 und danach wieder die Mittelpunkte in ihrer Eigenart mit zwei Ziffern von 20 bis 23 (siehe Bild unten).

Reihe(n) für Reihe(n) beziffert
Es folgt die nächste Reihe von außen nach innen. Im Prinzip, weil die innere Reihe auf der vertikalen Achse keine gegenüberliegende Seite haben kann erhalten auch diese Punkte zwei Ziffern als Bezeichnung (siehe Bild unten).

Innere Reihe nur Mittelpunkte
Krönung ist dann der Mittelpunkt der gleich 4 Ziffern von 32 bis 35 trägt (siehe Bild unten).

Absoluter Mittelpunkt
Inkscape User die sich für die Mathematik dahinter noch tief gehender Interessieren können im Inkscape-Wiki gerne in englischer Sprache mehr dazu nachlesen. Für die praktische Arbeit, um die gewünschten Punkte aufzufinden, reicht allerdings diese Beschreibung vollkommen aus.